At The Time Of The End

The eleventh chapter closes with the verses describing the final clash between the kings of the north and the south - since now we have the ingredients to put together the concepts of that which constitute north and south, we may proceed.

Now, the king of the north has shifted octals away from the "holy covenant" - which we initially realised in place as the separation of static subgroup and coset in the octal. There are two forms of triple remaining in that regard - now without the identity element (sent to {}) but yet with operations based on addition order two and the condition for subgroup addition A + B = (A v B)^c.

Thus a = {c,e,g} is now {} giving {a,e,g} + {a,c,e} = {e,g} + {c,e} = {c,g} using the cancellation modulo 2,

And {b,c} + {d,e} = {f,g} by (A v B)^c in the octal now comprised only of {b,c,d,e,f,g}.

Now the king of the north and south have ever been;

b = [b,d,f],[b,e,g],[a,b,c]
d = [a,d,e],[b,d,f],[c,d,g]
f = [a,f,g],[c,e,f],[b,d,f]

a = 1. = [a,b,c],[a,d,e],[a,f,g]
c = [a,b,c],[c,d,g],[c,e,f]
e = [a,d,e],[c,e,f],[b,e,g]
g = [a,f,g],[b,e,g],[c,d,g]

Yet in view in the north is a much greater diversity of elements - we have every combination of octal to consider in some extension field over the fields GF(4) and GF(8). We know that the king of the north comes like a whirlwind - in great numbers rather than alike the cyclic nature of an extension field over another field. Likewise we may recognise chariots as teams of horses (additive subgroups) and horsemen (a floating unity) and with many ships (static triples.) - "Countries" we will liken to cosets of the field GF(8) (as north and south were) rather than the former as of GF(4) - and there will be no combination of elements left standing apart - (for he overflows as if not with a "short orbit" of a subfield - which would mean every element in the north or south is present in one full cycle in the extensions order (the number of powers of its generators)).

Likewise then, there is an extension then in which both GF(8) and GF(4) are not both subfields. Yet then, we must assume that there is an additive subgroup containing our original octal (the glorious land where "those that understand" are given a "little help" and stand) so that in one orbit of the extension that particular additive group is present. (and is not a coset of a subfield).

That the "god of forces" does not gain its own form of multiplication (which was present only by the induced 3-cycle of the octals' multiplicative group) we see them only as they are reduced - as forms similar to K4 with their operations leeched from the octals. So be it! - lets see how the "god of forces" stands up (or doesn't).

There may be many orbits within an extension field - only small extensions of small order have one orbit of subgroups only - we see this in prime subfields, GF(4), GF(8) - but in high order fields GF(p,n) the number of additive subgroups of degree k is given by the product;

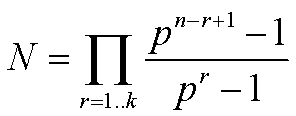
Which quickly outstrips the order of the extension field pⁿ. I.e. in most extensions there is more than one orbit.

Then the king of the north in operation is seen to be over every orbit of the groups in his ships of chittim as we had before - and the south over those cosets as {a,c,e,g} in the north (now static in the south) as we had before. (The south pushes at the north - we are in "northern territory").

Now, if GF(8) is a subfield of the extension F, then since C7 must be a subgroup of F* we conclude that any orbit of a K4 additive group that passes through one subgroup of GF(8) on its orbit, it must also by virtue of powers of the generator in its orbit pass through every subgroup of that octal. Since in our ships of chittim the following associations hold:

a = [a,b,c],[a,d,e],[a,f,g] and {c,e,g},{c,d,f},{b,e,f},{b,d,g}
b = [b,e,g],[b,d,f],[a,b,c] and {a,e,f},{c,f,g},{a,d,g},{c,d,e}
d = [b,d,f],[c,d,g],[a,d,e] and {a,b,g},{e,f,g},{b,c,e},{a,c,f}
c = [a,b,c],[c,d,g],[c,e,f] and {b,d,e},{a,e,g},{a,d,f},{b,f,g}
f = [a,f,g],[b,d,f],[c,e,f] and {a,c,d},{a,b,e},{b,c,g},{d,e,g}
g = [a,f,g],[b,e,g],[c,d,g] and {b,c,f},{a,b,d},{d,e,f},{a,c,e}
e = [a,d,e],[b,e,g],[c,e,f] and {d,f,g},{b,c,d},{a,c,g},{a,b,e}

In any extension field there is but one subgroup of any given order - it is unique: thus if the king of the north is traversing the column in the centre (the south, beginning {c,e,g}) then he is likewise traversing every column under the same subgroup of F* and we may assume that despite the ability to make unity float and passing through many other groups in the field F, there is no opportunity to cycle through the groups in each row at all.

For, if one row were instantiated as subgroups of F, so would every row and then there is no common seven cycle on them all! Yet the battle for the centre continues on.

The king "stretches forth his hand upon the countries" which we will take to mean the subgroups of every column are cycled.

We are told that the "land of Egypt will not escape". Thus. we pass through every subgroup of the southern octal in the order seven sub-cycle of the generators of F. Yet this is done by "the stretching forth of his hand" into an orbit that preserves the triples of the northern octal under the same seven cycle - but present as bows (triples) and not subgroups in F.

So, we conclude that not only is the northern octal not an additive subgroup of F, but that the southern octal must itself be a subfield! (because the southern octal has the same singletons as the "glorious land" {a,b,c,d,e,f,g} and is within the field F, present in all it's southern subgroups, but now within the realm (operation) of the south that pushed at him. (We have the north coming against the south and all are entered into by the north).)

He - the king of the north has power of the gold, silver and precious things of Egypt - the northern orbit that must pass through the southern "glorious land" also passes through the southern fortresses/subgroups - (where the riches are kept.)

Now, three escape out of his hand - which we may state are the three triples that oppose the triple [b,d,f] = a = 1 of the northern fortress but which are not part of the southern octal. (as there is only one correspondence to unity given [b,d,f] static therefore under the northern 7-cycle, a, c, e or g = 1)

Now, "countries" we may indeed liken to cosets of additive octal subgorups in F+, and these are present in orbits - and if there is a subfield isomorphic to GF(8) this does not impy there is only one orbit of octal groups in F+. Truly, octal groups may intersect in seven, three (or none) subgroups, so it is either the case that an octal is completely swept through (overflown) by horses and chariots (K4 subgroups in orbits) or is partially swept through by having three subgroups (or one subgroup or singleton) in intersection with the octal that passes through (or passes over).

By the cancellation law there is a unique element `g` sending an element x to h = xg in any group, we see how for every element y of every "country" in F there is a power of a generator that maps elements of [b,d,f]= H in its orbit to contain that certain element y in a coset g*H . (it "overflows and sweeps through") it may indeed "pass over" (grazing through) if g*[b,d,f] is not a subfield of the "country" - it will not conquer the whole country unless there is only one orbit of every subgroup isomorphic to K4 in that subfield, (i.e. the country is isomorphic to GF(8).) A necessary condition is that there be more than one orbit of the subgroups of F+ isomorphic to K4.

Now, if the king of the north uses the ships of chittim for his device then he may "stretch forth" to cycle through the other columns above - the text says "the land of egypt will not escape" and so we know the king of the north has this capability. In this fashion the king of the north may attack "from the sea."

The king of the north may attack without being defeated, so much so that he may travel "southward" and "westward" with impunity (As daniel would have written the columns above right to left) by stretching forth his hand over the "countries". When the southern stronghold falls, then the countries to the south and west are "at his steps (the king of the north's). In other words, as the king may do as he wills others capitulate to the same device. The king of the north in traversing rows is able to shift orbits - starting from the north through the ships of chittim by having intelligence with those that forsake the Holy covenant - even to the completion of the 1290 days over the seven cycles (one of every row) and the northern seven cycle.

When the south picks up the same device and can move into the north and the east without similar opposition (turning the page upside down if need be to write out rows and columns above) The king returns to fight an opponent from the south using his same device - and then positioned in the centre with only his god of forces to give him power, no one helps him and the device comes to an end.

We can state that the devices of man that are made from the "god of forces" in putting Christ's triune form into worldly structures has no further profit, th last manipulation has failed. Man is unable to construct His name because of the infinitely regressing perspective of God in trinity. The king comes to his end and there is none that can help him become superior to the opposition of the same device.

Continue To Next Page

Return To Section Start

Return To Previous Page