The Fifth Trumpet

We can also construct models similar to the trinity model using other finite fields. Multiplication does indeed send additive subgroups to additive subgroups in finite fields - more often than not into cycles of length or order similar to the order of the cyclic multiplicative group, but sometimes, when the additive subgroup is a multiplicative coset of a subfield or wholly comprised of cosets of subfields we have a reduced length orbit of these additive subgroups - equal in length to the index of the constituting subfield.

For instance, GF(16) has 35 K4 additive subgroups. It has two orbits of length 15, and one orbit of length 5, which is comprised of cosets of the subfield isomorphic to GF(4).GF(27) has 13 additive subgroups isomorphic to C3 x C3, and has one such orbit of length 13.

The orbits in all instances can be acted upon by the frobenius map: which sends additive subgroups to other additive subgroups, according to their fixed fields. The action is like a "twisting" between orbits that are not cosets of fixed fields, and can "jump" from one orbit to another, as well as permute elements within orbits that are of short length. The maths is quite simple, and a C++ program I wrote can find the number of orbits and their length - but for large fields I gained very little workable information on the action of frobenius on this twisting of one orbit to another due to computation time. What we can say about frobenius is that it has a cyclic Galois group associated with it and the orbits can be permuted cyclically under frobenius.

As every additive subgroup is a collection of order p subgroups isomorphic to the prime subfield, we may separate terms so that if the prime subfield is "W" then any additive group G is comprised of subgroups xW for x in some set of generating factors X. The position of the additive subgroup in its orbit is determined then by some element y in the extension field's multiplicative group, and the final "twisting" of the orbit under the frobenius map (holding some subfield K = {xW : x in X} is taken from the set of prime powers up to the degree of the extension field. Then, every p-order subgroup "element" is described by (w*x*y)^z, where w is in W, x in X and y in Y (the multiplicative group of the extension field).

The locusts have faces like those of men - in appearance they are even as singleton elements similar to those of GF(8)*. Their appearance is to confuse the route out of laodicea shown by the circuit of the angel - we see "men" are a representation of the singletons that are as much a generator of the mystery of the seven candlesticks as the seven spirits are generators of the churches (wherein men are).

We can equate the "teeth as lions" to the letter "W"

The "breastpolates of iron" to the letter "X"

The "wings" to the letter "Y"

The "tails like scorpions" to the letter "Z".

The following content drops these assertions - I hope this does not confuse!

Now, it is true that God does not appoint His elect to wrath, but satan reads his bible too. The enemy knows that the elect in Philadelphia and the action of Christ's victory on the cross limits his ability to work against the Holy Spirit. We can then on the basis of the five churches (as foolish virgins), construct a little action from finite fields in all their complexity to fill the description of the locusts from the bottomless pit - the methods used by spiritual wickedness to draw men away from the Holy Spirit of God and into disobedience.

Consider an octal with one subgroup fixed and the other elements marked as X1 to X5.

[0,a,b,X1,X2,X3,X4,X5]

Now, given a seven cycle we can generate a specific octal from these elements a,b. The action of the locusts is to permute X1,X2,X3,X4 and X5 to confuse the seven cycle. This is fuel for the fire of the sixth trumpet - as these are described as "horses" upon which the work of the sixth trumpet spirits rest as horsemen. Horsemen are then additive subgroups in the extension field.

We can use a fixed field F under a frobenius automorphism to take the place of what could be the element "c" and use its cosets of its additive group under frobenius to permute the remaining elements X2 to X5, thus apparently changing the seven cycle (or equivalently the octal under it.)

We can also use larger cosets, with X1 to X5 separated in the midst of all the finite field's elements so if extra additive groups are labelled W, The additive subgroups are arranged as this.

{0,a,b,F=X1,W,W,W,X2,W,W,W,X3,W,W,W,X4,W,W,W,X5,W,W,W}

keeping the subfield F fixed would permute the elements X2 to X4 within themselves (under frobenius), likewise if {F,W,W,W} is also a subfield then we may have a short orbit that permutes F=X1 to X5 holding F fixed but this changes the orbit of {F} amongst {F,W,W,W}.

The idea would then be for F a subfield of a subfield K where K is {F,X1,X2,X3,X4} then frobenius on the whole field holding F fixed will permute the X's amongst themselves with the W's between them as above. In this way we have a cyclic curling appearance to the multiplicative cosets of the additive groups (which are also groups), much like the curls of "women's hair".

We can also take the whole field {F=X1,W,W,W,,X2,W,W,W,X3,W,W,W,X4,W,W,W,X5,W,W,W} and use a much greater extension field over this one and preserve the structure - all the way up to algebraic closure. The orbit would depend on a subfield's index in the multiplicative group - its cosets would form a factor group, which additively could be isomorphic to GF(16) for example, giving another short orbit of length 5.

For brevity we will just note that the action of the locusts is to be used to disguise the divine seven cycle. Since two elements of any group of seven cycles {0,a,b,c,d,e,f,g} can be picked arbitrarily (here ab say) and then an element defined (ab????,...) that will generate the group: we are given that we are only interested in the symbols F = X1 to X5, and also in the symbols W.

We will refer to any structure under the frobenius map looking like;
{ F=X1,W,W,W,X2,W,W,W,X3,W,W,W,X4,W,W,W,X5,W,W,W} as simply Z.

When the trinity model was made, I stated that there could also be other models, but these are divergent, having more subgroups than elements or less subgroups in the smaller cases. This huge divergent system we will call "the bottomless pit" since it could be described to be completely unbounded, unlike the fields GF(2),GF(4) and GF(8).

We will describe the star that falls as having this "method" to permute the symbols X1 etc (the key to the bottomless pit) The pit is open spiritually, and the "smoke" that comes out darkens (obscures) the air (breath - spirit) as smoke from a great furnace (many different resultant octals is not the answer - but the great furnace would be a potentially infinite number of finite fields all characteristic 2, that can be used to permute any number of elements (Except a simple transposition). Thus the "sea" has been enlarged) The sun, (the original octal group) is now "confused" or rather "obscured" by having its operations altered by these overlaid permutations.

John describes these cosets of additive groups of finite fields as "locusts", given power (under frobenius) to twist men in agony. They are commanded not to hurt any green thing or tree, (i.e. the singletons in the seven cycle and the corresponding triples in the left hand. They must be intact but permuted in "five-cycles" or less, but not transpositions, they as "sets of elements" must not "mix". This is to be deception, not opposition outright.) The seal of God corresponds to whomsoever dwells within the churches and listens to the Holy Spirit, and is not swayed by these demonic attributes. We can take the seal of God to mean that if the elements (d,g) in the octal and seven cycle (a,b,d,c,f,g,e) are permuted (swapped), then they are in their operations also as to not confuse the set of operations but to simply relabel and make it isomorphic as to before.

It is given then that either the frobenius map has an order a multiple of five or some subfield an orbit of length five, and the torment is to permute cyclically - like the sting of a scorpion that causes a limb to twist. Men seeking death shall not find it - because the permutation of the four elements X1 to X4 is simply defined under a different octal. Neither is there any escape from the system. The finite fields structure is completely sound, so when this judgement comes there will not be a simple way out when the system is closed (see the two witnesses and the earthquake wherein a tenth of the city falls).

The shape of the locusts John saw are described as horses arrayed to battle, lined up as cosets of the same additive subgroup: X1,X2,X3,X4,X5 etc (but the locusts themselves look more like WWWWWWWWWWWWWWWW........) describing the cosets of subfields akin to "crowns like gold" - the subfield itself (The heads or subfields being akin to the trinity model), having faces like the faces of men. (I.e. the fixed field F under frobenius is aligned with what would be the element "c") this gives rise to the permutation of the elements X1 to X5 within themselves.

We see then that the set of X1 to X5 is a leading edge set: so that the "W" symbols follow after. As the 'W's are somewhat extraneous and the "faces" X1 to X5 do not have a W amongst their permutations, The trailing cosets of W between each "X" would trail like twisting women's hair in the array of additive cosets under cycle by multiplying by a generator. They would appear to twist like curls under the action of frobenius.

The "hair like women's hair" is explained by the orbits of the subgroups (as horses arrayed unto battle, or viewed side by side) and the elements of the field in that cycle as acted upon by a generator of the field's multiplicative group. In the following image, a short orbit of K4 subgroups is assumed, (and hence the orbit is short if F has a subfield of order four.) We see that at the ends of a cycle, the effect is much like braiding or appears as "women's hair".

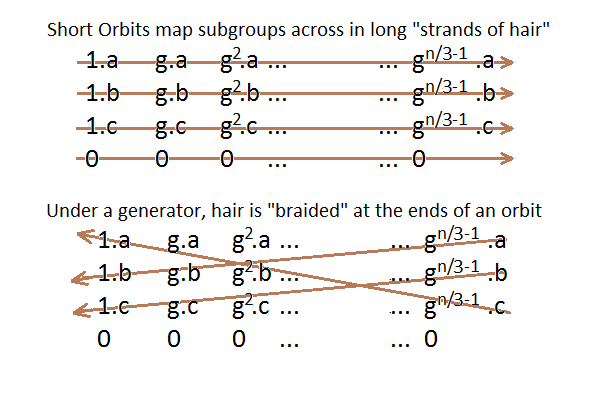
The teeth like lions, would show that the symbols X1 to X5 are arrayed as the subgroups under which [0,a,b,c] would be permuted by frobenius as the lion of Judah. (There are two sets: under frobenius in the octal which permutes the elements properly [0,a,b,c] to [0,a,d,e] to [0,a,f,g] (Which is the action of the Lion of Judah opening the last three seals) and a second set of the symbols {d,e,f,g} being permuted - which looks similar but can change the octal structure. Their "teeth" are that which does the damage. (in the sixth trumpet) the prime subfield used.

They are described as having breastplates of iron. (protection) The finite fields are structurally sound and are used for most encryption systems on the internet - particularly public key systems. - there is no breaking it with an antidote without huge effort. There is no moving the element's orbits themselves without the "power" to rearrange them under frobenius - described as sets of horses (cosets) in chariots (X1,W,W,W for instance as above) their rearranging in Johns vision rearranged every one of these "chariots" simultaneously - it must have been noisy in the vision. The additive group W,X1,X2,X3,etc forms a group denoted simply by "X" - which is a "breastplate" as it were.

The position in the cycle is determined by a product of X by a generator, we take the multiplicative subgroup of the field that generates the orbit to be y from the set of all such generators "Y" - whcih has the appearance of a pair of wings.

They had tails like scorpions. Here, we consider the possible Galois fields over our field Z, all the way up to algebraic closure. These sets are like scorpions that preserve the "power" of the fixed field F under frobenius (Z is now a subfield as is F) and all these extensions permute the elements X1 to X5 holding F fixed (i.e., torment for five months). Using a subfield of F would twist the elements under the locusts constituting F, but would send F to itself as F is an extension comprised of additive cosets itself. Thus extensions are like scorpions that cause the sets within F to twist when chosen correctly.

Then, over all of them is algebraic closure - represented here by the "destroyer" Apollyon or Abaddon

But wait!! It gets worse!!

Why do we need to permute five symbols? We could just permute four or three of the X's as well, Using our fixed field F appropriately. If the seal of God is such that permutations of the elements are carried into the seven cycles so that we simply relabel elements, keeping every operation secure then we can expect that we could also move F further to the right so we permute the set in four or three-cycles (but not two, for why see later.)

{a,b,c,F=X1,X2,X3,X4} i.e., "d" is taken place by F.

I guess that this would depend on who the individual chose to listen to,.. the Holy Spirit or a vast and bothersome bunch of locusts.

We are told that "Men shall seek death and shall not find it, and desire to die and death shall flee from them." We see that in the churches the desire is to construct the devices of satan of the first four seals over the four churches to whom the star with the key to the pit fell, as "to the earth". The devices themselves fail when used to construct a fourth dialectic "bow": The apparatus of these locusts is to create the image to the beast - the woman riding the scarlet beast - an artifical construct that mimics the sinful carnality of a persons senses. This attempt is so that it may take the place of an artificial "bow" in the place of what would be considered "Death's" own position. With that image or "Hell" that follows after, there is in position a false "balance" in place of "Death". We see the woman's (the image's) construction taking shape.

Continue To Next Page

Return To Section Start